Représentation vectorielle d’un plan donnée par ses traces

Pour donner une équation d’un plan, on doit connaître les coordonnées d’un point du plan (x₀ ; y₀ ; z₀) ainsi que les composantes de deux vecteurs parallèles au plan (x_v1 ; y_v1 ; z_v1 et x_v2 ; y_v2 ; z_v2) :

$\dpi{120} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix}+k \begin{pmatrix} x_v_1 \\ y_v_1 \\ z_v_1 \end{pmatrix}+l \begin{pmatrix} x_v_2 \\ y_v_2 \\ z_v_2 \end{pmatrix}$

Ces informations peuvent être obtenues en observant les traces du plan.

Tous les points qui se trouvent sur les traces d’un plan appartiennent au plan . Les coordonnées d’un de ces points peuvent être utilisées comme x₀, y₀ et z₀ dans l’équation du plan. Si vous avez le choix, sélectionnez le point avec le plus de coordonnées nulles.

Pour déterminer les composantes des deux vecteurs, on peut procéder de la manière suivante : déterminer les coordonnées de trois points sur les traces et calculer les composantes de deux vecteurs reliant ces points (voir équation d’un plan passant par trois points).

Voici un exemple. Sur le schéma ci-dessous, le plan α est représenté par ses traces :

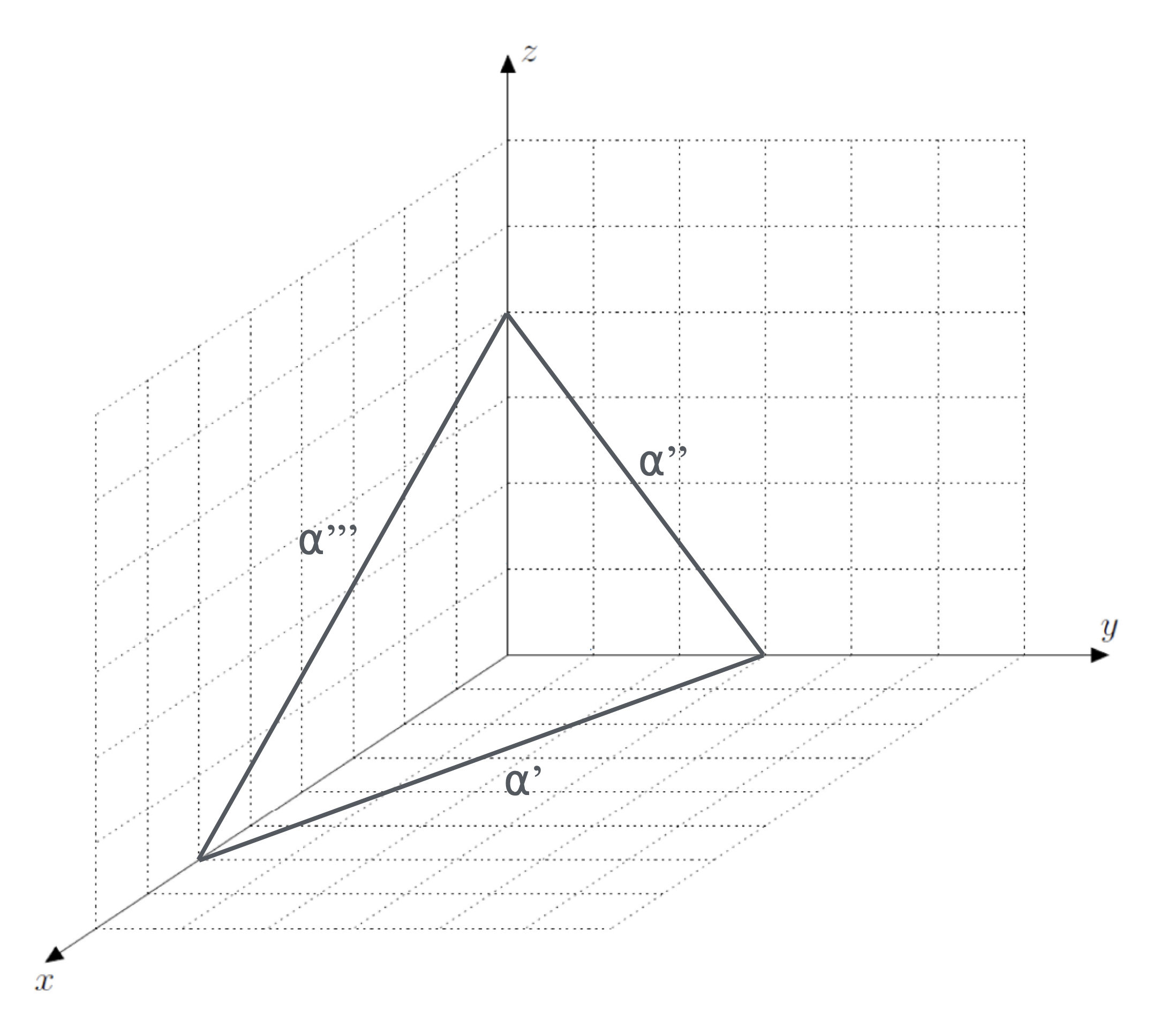
On peut utiliser par exemple les coordonnées des points d’intersection du plan avec les axes du repère (points A(6; 0; 0), B(0; 3; 0) et C(0; 0; 4)).

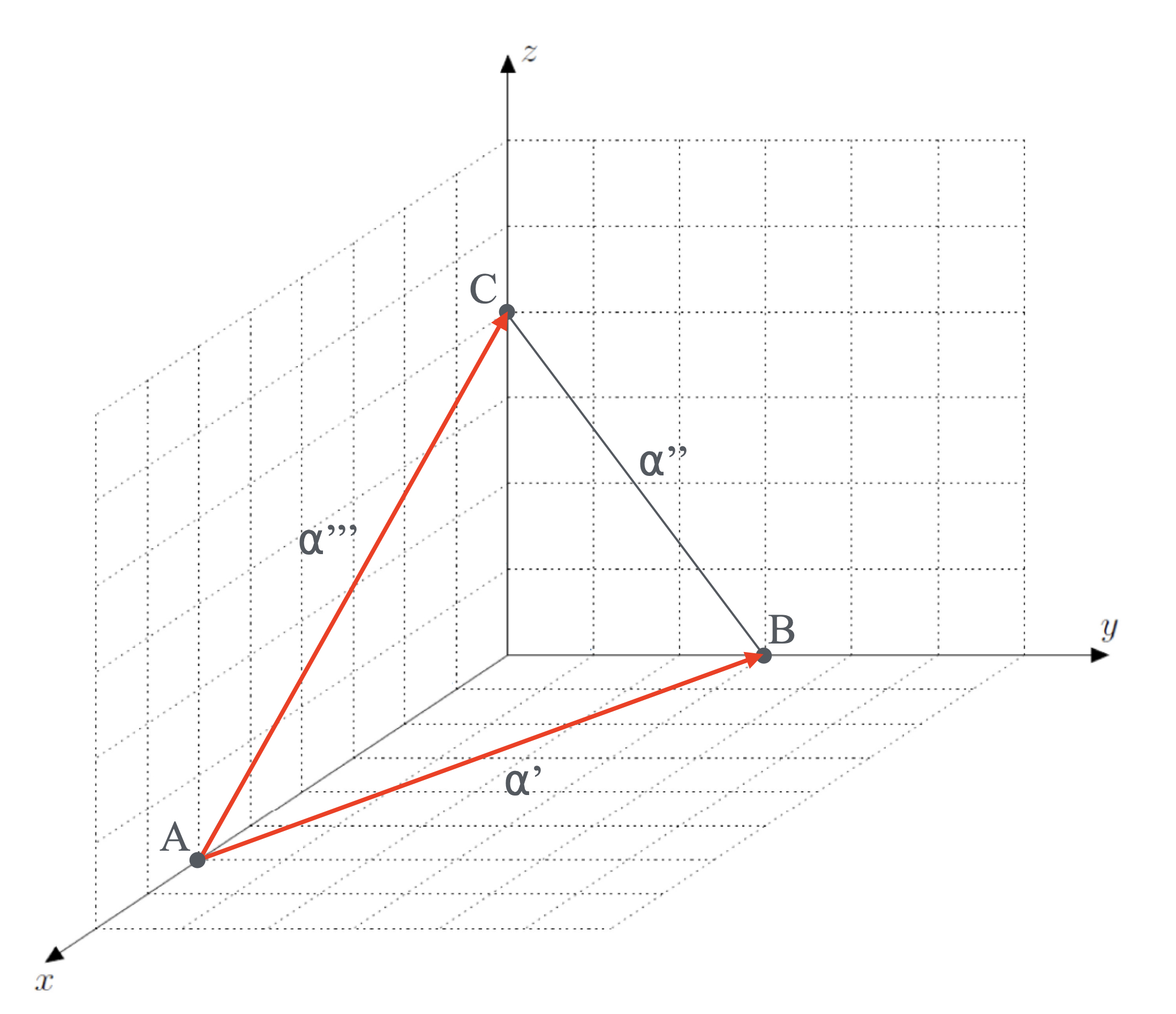
On peut utiliser un de ces points comme x₀ ; y₀ et z₀. Ici on utilisera le point A(6; 0; 0). Ces points définissent des vecteurs comme le vecteur AB, AC, BC, BA etc. Deux de ces vecteurs suffisent pour déterminer l’équation de ce plan. Ici on utilisera les vecteurs AB et AC :

$\overrightarrow{AB}=\begin{pmatrix} x_B-x_A \\ y_B-y_A \\ z_B-z_A \end{pmatrix}= \begin{pmatrix} 0-6 \\ 3-0 \\ 0-0 \end{pmatrix}= \begin{pmatrix} -6 \\ 3 \\ 0 \end{pmatrix}$

$\overrightarrow{AC}=\begin{pmatrix} x_C-x_A \\ y_C-y_A \\ z_C-z_A \end{pmatrix}= \begin{pmatrix} 0-6 \\ 0-0 \\ 4-0 \end{pmatrix}= \begin{pmatrix} -6 \\ 0 \\ 4 \end{pmatrix}$

Ces informations permettent de donner une équation du plan α:

$\alpha : \begin{pmatrix} x \\ y \\ z \end{pmatrix}=\begin{pmatrix} 6 \\ 0 \\ 0 \end{pmatrix}+k \begin{pmatrix} -6 \\ 3 \\ 0 \end{pmatrix}+l \begin{pmatrix} -6 \\ 0 \\ 4 \end{pmatrix}$

On peut aussi écrire cette équation sous forme d’un système de trois équations:

$\alpha :\left\{\begin{matrix} x=6-6k-6l \\ y=3k \;\;\;\;\;\;\;\;\;\;\;\;\;\; \\ z=4l\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \end{matrix}\right.$

Notez que les composantes de deux vecteurs peuvent être déterminées directement sur le schéma.

Parfois, il est possible d’utiliser les vecteurs unitaires parallèles aux axes du repère:

Un plan vertical (parallèle à l’axe Oz) est parallèle au vecteur vertical $\inline \small \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$ . et un plan horizontal est parallèle aux vecteurs $\inline \small \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$ (parallèle à l’axe Ox) et $\inline \small \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}$ (parallèle à l’axe Oy).

Voici un exemple :

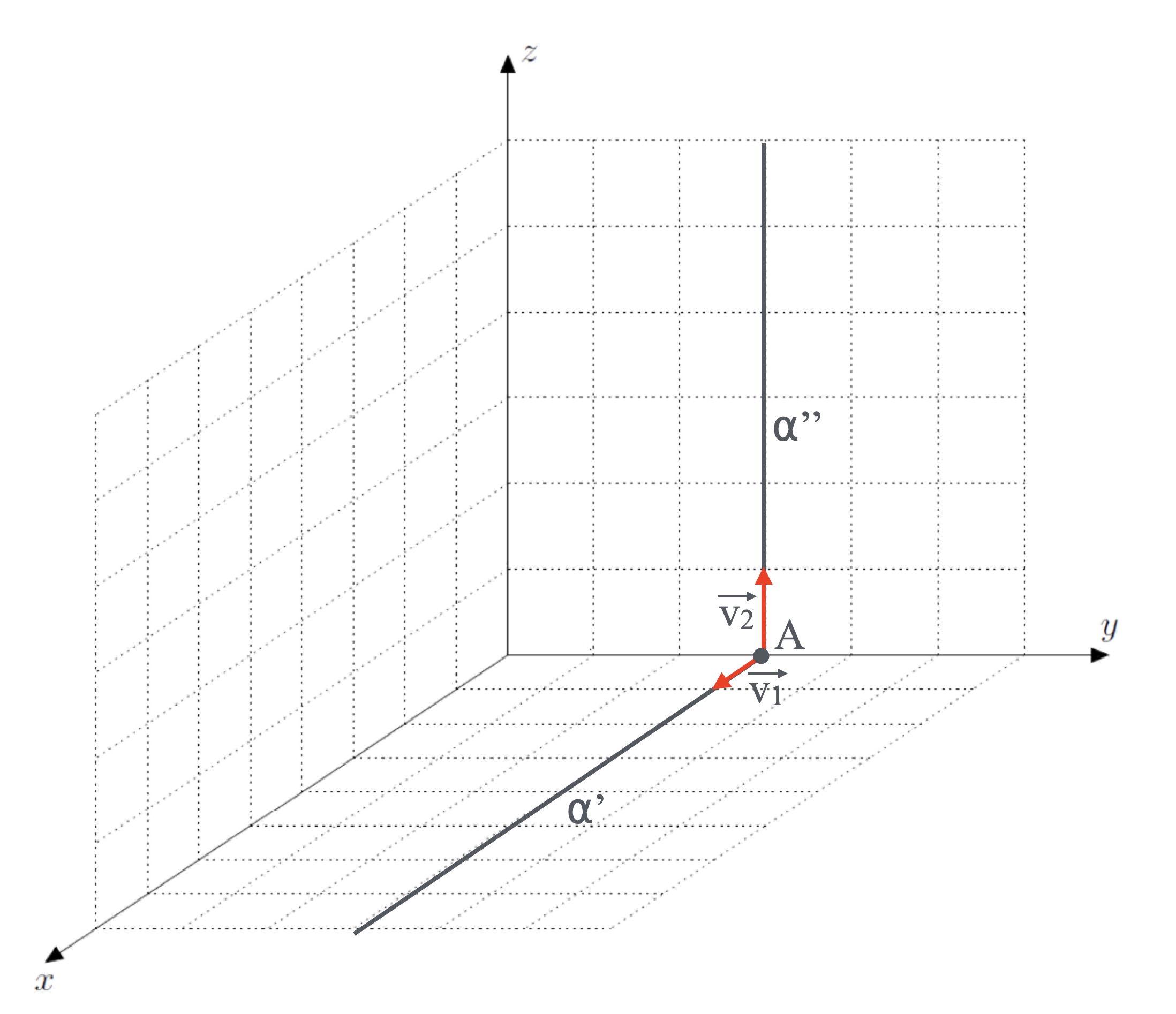
Ici on peut utiliser le point A(0; 3; 0) comme x₀ ; y₀ et z₀et les vecteurs unitaires $\overrightarrow{v_1}\begin{pmatrix} 1\\ 0 \\ 0 \end{pmatrix}$ et $\overrightarrow{v_2}\begin{pmatrix} 0\\ 0 \\ 1 \end{pmatrix}$ .

Une équation du plan est ainsi obtenue:

$\alpha : \begin{pmatrix} x \\ y \\ z \end{pmatrix}=\begin{pmatrix} 0 \\ 3 \\ 0 \end{pmatrix}+k \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}+l \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$